구간 트리, 세그먼트 트리 (Segment Tree), 자바스크립트로 구현

 

 

💡세그먼트 트리, 구간 트리 (Segment Tree)

 

여러 개의 데이터가 연속적으로 존재할 때 특정한 범위의 데이터의 합을 가장 빠르고 간단하게 구할 수 있는 자료로 세그먼트 트리가 있다. 구간 트리는 배열의 특정 구간에 대한 질의를 빠르게 하기 위해 사용될 수 있다. 구간 트리는 주어진 배열의 구간들을 표현하는 이진 트리를 만든다. 루트는 배열의 전체 구간을 표현하고, 한 트리의 왼쪽 자식과 오른쪽 자식은 해당 구간의 왼쪽 반과 오른쪽 반을 표현한다. 각 노드는 해당 구간에 대한 계산 결과를 저장해둔다. 

 

 

✓ 특정 구간의 합을 가장 빠르게 구하는 방법은?

예시 데이터 : 1 9 3 8 4 5 5 9 10 3 4 5

 

💻 방법1. 단순 배열을 이용해 선형적으로 구하기

 

0	1	2	3	4	5	6	7	8	9	10	11
1	9	3	8	4	5	5	9	10	3	4	5

 

데이터의 개수는 12개이므로 인덱스는 0부터 11까지 차례대로 들어간다. 하나씩 앞에서부터 더하면 되는데 데이터의 개수가 N 개라고 하면 시간 복잡도는 O(N)이 되는 것이다. 이러한 방식을 사용해도 결과를 얻을 수 있지만 구간의 합을 구하는 속도가 너무 느리기 때문에 좋은 알고리즘이라고 볼 수 는 없다.

 

 

💻 방법2. 트리 구조를 이용해 구하기

 

세그먼트 트리를 이용해 합을 구하면 시간 복잡도는 O(logN) 으로 줄어든다. 

 

 

1) 구간 합 구하기

 

인덱스는 방법 1과 동일하게 0 부터 11까지이다. 빠르게 합을 구하기 위해서는 구간 합트리를 새롭게 생성해 주어야 한다. 최상단 노드에는 전체 원소를 더한 값이 들어간다.

 

 

두 번째 노드와 세 번째 노드도 마찬가지로 하위 노드를 다 더한 값을 가지게 된다. 원래 데이터의 범위를 반씩 분할하여 그 구간의 합들을 저장하도록 초기 설정을 하는 것이다. 이러한 과정을 반복하면 구간 합 트리의 전체 노드를 구할 수 있다.

 

 

이러한 방식으로 구간 합 트리를 구하게 되면 아래와 같이 나온다. 데이터의 인덱스는 0부터 시작하지만 구간 합 트리에 한해서는 인덱스 번호가 1부터 시작한다. 이렇게 되면 2를 곱했을 때 왼쪽 자식 노드를 가리키므로 효과적이다.

 

 

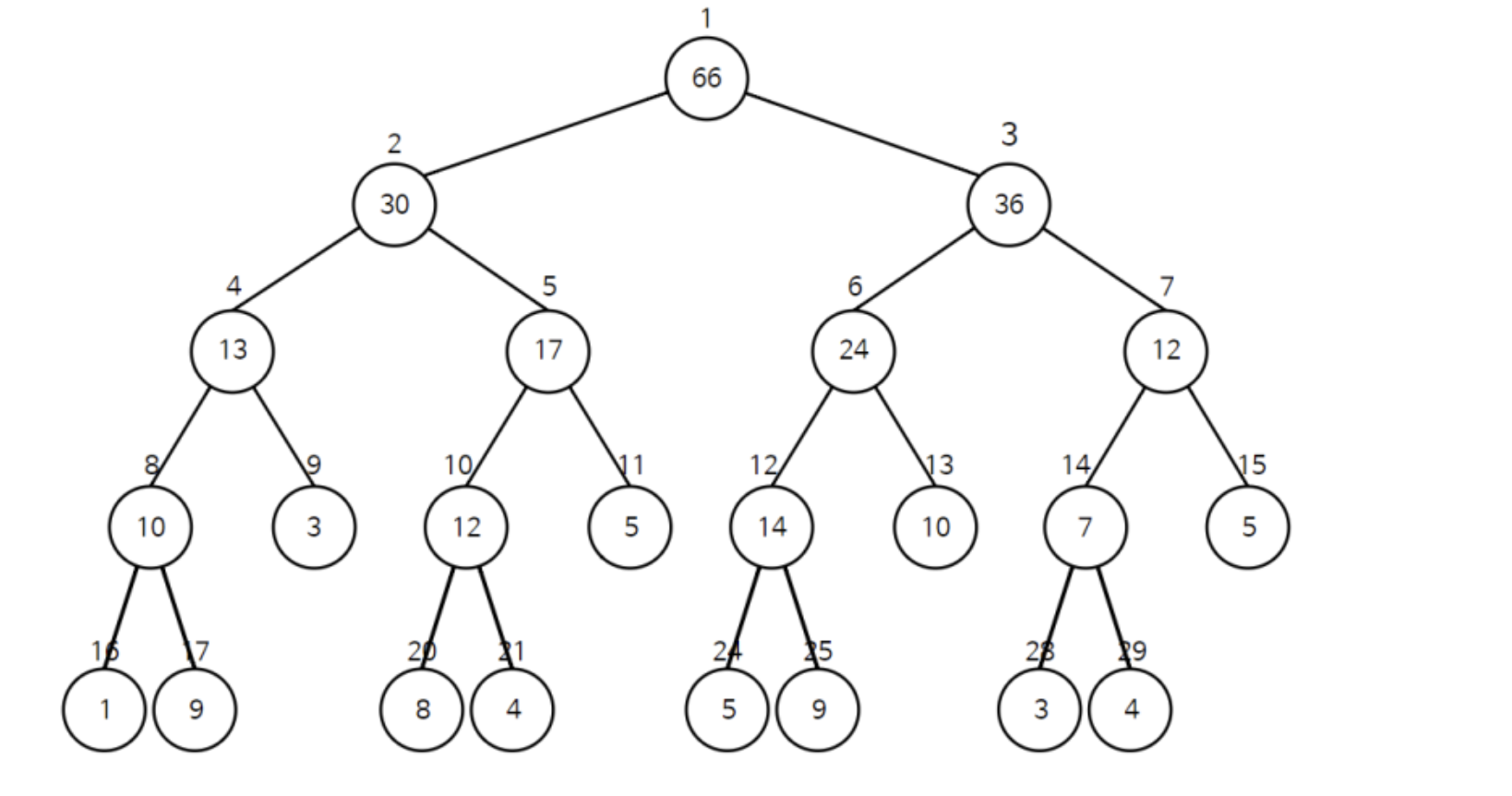
✓ 구현하는 법

 

구간 트리의 기본적인 구현의 원리는 다음과 같다. 주어진 구간을 반씩 쪼개어 트리 자료구조를 생성하는데, 더 이상 쪼갤 수 없게 되면 요구되는 조건에 따라 최소값, 최대값, 또는 구간의 합을 차례로 채워나간다. 아래의 코드는 객체로 구현한 최소값을 구하는 구간 트리이다.

 

const createSegmentTree = (arr, start, end) => {
  
  // 만약 시작점과 끝점이 같다면 해당하는 값을 리턴한다.
  // 재귀 함수로 구현했기 때문에 base case 에 해당한다.
  if (start === end) return { value: arr[start] }
  
  // 시작점과 끝점이 같지 않다면 중간점을 찾아 2개의 구간으로 나눈다.
  let middle = Math.floor((start + end) / 2);
  
  // 중간점을 기준으로왼쪽과 오른쪽으로 분리한다.
  let left = createSegmentTree(arr, start, middle);
  let right = createSegmentTree(arr, middle + 1, end);
  
  // 현재 구간의 값을 value 에 넣고, 나뉜 구간을 각각 왼쪽과 오른쪽 노드로 나누어 할당한다.
  return {
    value: Math.min(left.value, right.value),
    left,
    right
  }
}

 

[ 출력결과 ]

 

예시데이터: const arr = [2, 5, 1, 4, 9, 3];

 

예시 데이터: const arr = [1, 9, 3, 8, 4, 5, 5, 9, 10, 3, 4, 5];

 

 

✓ 원하는 구간을 찾는 방법

 

// rs 와 re 는 각각 구간의 시작점과 끝점
const findMinInTree = (start, end, rs, re, tree) => {
    // 트리와 노드의 구간이 일치하거나 tree 가 구간 안에 포함되는 경우
    if (rs <= start && end <= re) return tree.value;

    // 구간과 트리가 겹치지 않는 경우
    if (end < rs || start > re) return Number.MIN_SAFE_INTEGER;

    // 겹치는 부분이 있는 경우
    const middle = Math.floor((start + end) / 2);
    return Math.max(
        findMinInTree(start, middle, rs, re, tree.left),
        findMinInTree(middle + 1, end, rs, re, tree.right)
    );
};